批标准化,相当于深度学习中的数据归一化。
普通机器学习的归一化只针对输入层,而BN对中间每一层输入(激活函数处理前的数值,我称之为net值)进行归一化。
归一化的目的是使的数据的分布集中在激活函数的敏感区域(即中间线性区域)。
BN层就是对深度学习的中间层的输入数据(net值)进行归一化,解决在训练过程中,中间层数据分布发生改变的情况,使得每一层的分布相似(标准正态),同时引入非线性, 保留原来每层训练得到的特征分布(通过变换重构)。
机器学习领域的重要假设:独立同分布假设,即假设训练集数据和测试集数据是满足相同分布的,这是通过训练数据获得的模型能够在测试集获得好的效果的一个基本保障。
BatchNorm就是在深度神经网络训练过程中使得每一层神经网络的输入保持相同分布的。
Mini-batch 相对于 SGD的两个优点:梯度更新方向更准确;并行计算速度快。
BatchNorm就是基于mini-batch的,这也是名称中Batch的由来。
随机梯度下降成了训练深度网络的主流方法。尽管随机梯度下降法对于训练深度网络简单高效,但是它有个毛病,就是需要我们人为的去选择参数,比如学习率、参数初始化、权重衰减系数、Drop out比例等。这些参数的选择对训练结果至关重要,以至于我们很多时间都浪费在这些的调参上。
采用Batch Normalization的好处
提升了训练速度,收敛过程大大加快。
(1)你可以选择比较大的初始学习率,让你的训练速度飙涨。以前还需要慢慢调整学习率,甚至在网络训练到一半的时候,还需要想着学习率进一步调小的比例选择多少比较合适,现在我们可以采用初始很大的学习率,然后学习率的衰减速度也很大,因为这个算法收敛很快。当然这个算法即使你选择了较小的学习率,也比以前的收敛速度快,因为它具有快速训练收敛的特性;
(2)你再也不用去理会过拟合中drop out、L2正则项参数的选择问题,采用BN算法后,你可以移除这两项了参数,或者可以选择更小的L2正则约束参数了,因为BN具有提高网络泛化能力的特性,避因为这是类似于dropout的一种防止过拟合的正则化方式;
原因:均值和方差是在mini-batch上计算的,而不是在整个训练集,因此均值和方差会存在噪声,所以和dropout类似,它往每个隐藏层的激活值上增加了噪音:dropout增加噪音的方式,使一个隐藏的单元,以一定的概率乘以0. 但因为添加噪音较小,因此正则化效果轻微,可以和dropout一起使用。
(3)再也不需要使用局部响应归一化层了(局部响应归一化是Alexnet网络用到的方法,搞视觉的估计比较熟悉),因为BN本身就是一个归一化网络层;
(4)可以把训练数据彻底打乱(防止每批训练的时候,某一个样本都经常被挑选到)。
深度神经网络中的归一化问题 Internal Covariate Shift:
原因在于神经网络学习过程本质就是为了学习数据分布,一旦训练数据与测试数据的分布不同,那么网络的泛化能力也大大降低;另外一方面,一旦每批训练数据的分布各不相同(batch 梯度下降),那么网络就要在每次迭代都去学习适应不同的分布,这样将会大大降低网络的训练速度,这也正是为什么我们需要对数据都要做一个归一化预处理的原因。
我们知道网络一旦train起来,那么参数就要发生更新,除了输入层的数据外(因为输入层数据,我们已经人为的为每个样本归一化),后面网络每一层的输入数据分布是一直在发生变化的,因为在训练的时候,前面层训练参数的更新将导致后面层输入数据分布的变化。以网络第二层为例:网络的第二层输入,是由第一层的参数和input计算得到的,而第一层的参数在整个训练过程中一直在变化,因此必然会引起后面每一层输入数据分布的改变。我们把网络中间层在训练过程中,数据分布的改变称之为:“Internal Covariate Shift”。
BN概述
基本思想:
深层神经网络在做非线性变换前的激活输入值net值随着网络深度加深或者在训练过程中,其分布逐渐发生偏移或者变动,之所以训练收敛慢,一般是整体分布逐渐往激活函数的取值区间的上下限两端靠近,导致反向传播时底层神经网络的梯度消失,这就是深层神经网络收敛越来越慢的原因。
BN就是通过规范化手段,把每层神经网络任意神经元输入值net值的分布强行拉回到均值为0方差为1的标准正态分布,使得激活输入值落在中间比较敏感的区域的概率较大,让梯度变大,避免梯度消失问题,梯度变大意味着学习收敛速度快,加快训练速度。
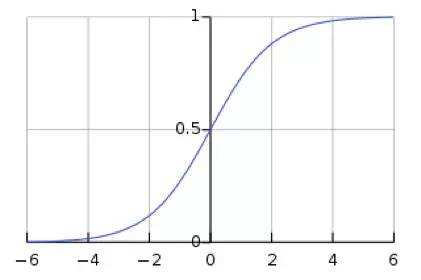
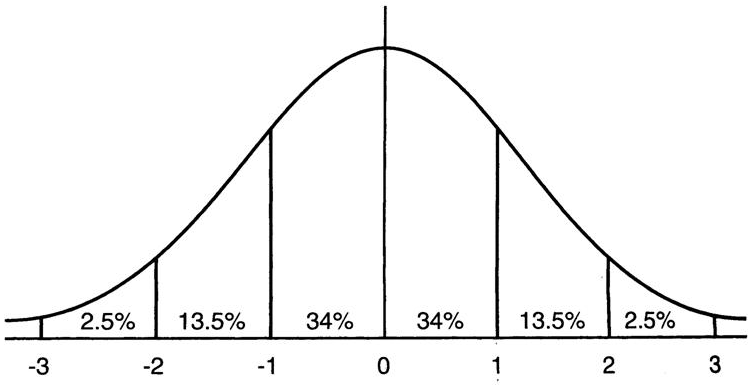
如图,转换为标准正态分布后,数据落在-4,4的概率变大,而在这个区间范围内,对应的激活函数的梯度较大。
但是:由于数据都落在了激活函数的线性区域,相当于做了线性变换,那么整个网络就会变成多层线性网络,表达能力下降。为了解决这个问题,BN为了保证非线性的获得,对变换后满足均值为0方差为1的x又进行了scale加上shift操作(y=sclae*x + shift),而这两个参数是通过训练学习得到的,意思是通过scale和shift把这个值从标准正态分布进行一些移动和变形,使得数据的散落区域从正中心向非线性区间进行部分移动。
训练
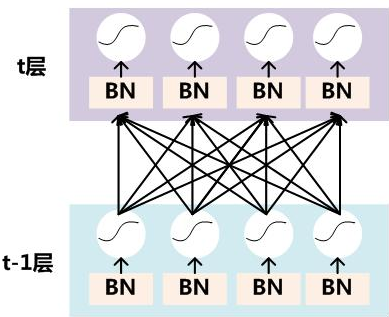
就像激活函数层、卷积层、全连接层、池化层一样,BN(Batch Normalization)也属于网络的一层。
BN层是对每个隐层的net值进行变换。经过BN变换以后的值再进过激活函数得到out值。
对于mini-batch来说,一次训练包含m个训练样本,因此对于隐层的每个神经元的激活值来说包括:
预处理:
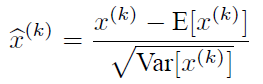
注意:这里t层第k个神经元的并不是指原始输入,而是该神经元隐层的net值的第k维数据。
变换的意思是:某个神经元对应的net值减去mini-batch内m个样本在该层对应维度神经元的m个net值的均值并除以方差。也就是说,这个变换和标准归一化一样,对每个样本的每个维度的归一化需要所有样本该维度的数据。
某个神经元的net值在经过变换后就会形成服从均值为0,方差为1的正态分布。
为了避免数据始终落在激活函数的线性区域,导致网络的表达能力下降,因此引入两个调节参数scale和shift,对变换后的net值进行变换的反操作
引入了两个可学习参数γ和β:
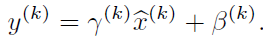
每一个神经元$x^k$都会有一对这样的参数γ、β。这样其实当:
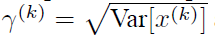
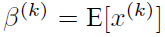
是可以恢复出原始的某一层所学到的特征的。因此我们引入了这个可学习重构参数γ、β,让我们的网络可以学习恢复出原始网络所要学习的特征分布。最后Batch Normalization网络层的前向传导过程公式就是:

上面的公式中m指的是mini-batch size。
预测阶段
训练阶段可以根据mini-batch的若干个样本进行变换。
但是测试阶段我们一般只输入一个测试样本。我们可以采用所有训练实例中获得的统计量来代替mini-batch中m个训练实例的均值和方差统计量。
计算全局统计量时只需利用每次mini-batch计算的均值和方差统计量,不需要重新计算, 这里方差采用的是无偏方差估计。
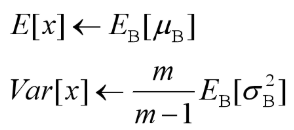
有了均值和方差,并且每个隐层scaling和shift参数已经计算好,在预测时就可以采用:
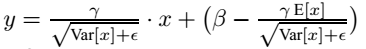
这个公式其实和:
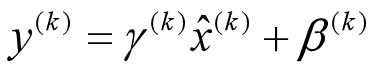
等价,就是代入而已,不过实际计算时可以减少计算量。
参考:
BN详细笔记:https://www.cnblogs.com/guoyaohua/p/8724433.html
Batch normalization 学习笔记:https://blog.csdn.net/hjimce/article/details/50866313
批标准化过程:https://blog.csdn.net/whitesilence/article/details/75667002